This week I had the pleasure of attending a seminar talk Nick Vlamis gave at CUNY, where he taught us a very pretty trick due to Anderson which one can use, as Anderson did, to prove that the groups of orientation-preserving homeomorphisms of the $2$ - and $3$ -spheres are simple. The purpose of this post is to reproduce Nick’s exposition of the trick.
Suppose $g$ is a homeomorphism of a surface $S$ (for me a surface is a Hausdorff and second countable $2$ -manifold) whose support
$\operatorname{Supp}(g) = \overline{\{x \in S : g(x) \ne x\}}$is contained in the interior of some closed disk $D$ in $S$ . Since $\operatorname{Supp}(g)$ is closed, there is in fact some closed disk $\Delta$ properly contained in $D$ and containing $\operatorname{Supp}(g)$ . In fact, we can find a countable sequence of disjoint disks $\{\Delta_n\}_{n \in \mathbb{Z}}$ with $\Delta = \Delta_0$ , each contained in the interior of $D$ . Since a sequence of points, one from each disk must have a limit point in $D$ , why don’t we arrange the $\Delta_n$ to Hausdorff converge to a point $x_{+\infty}$ as $n \to +\infty$ and a point $x_{-\infty}$ as $n \to -\infty$ . Here’s the picture.
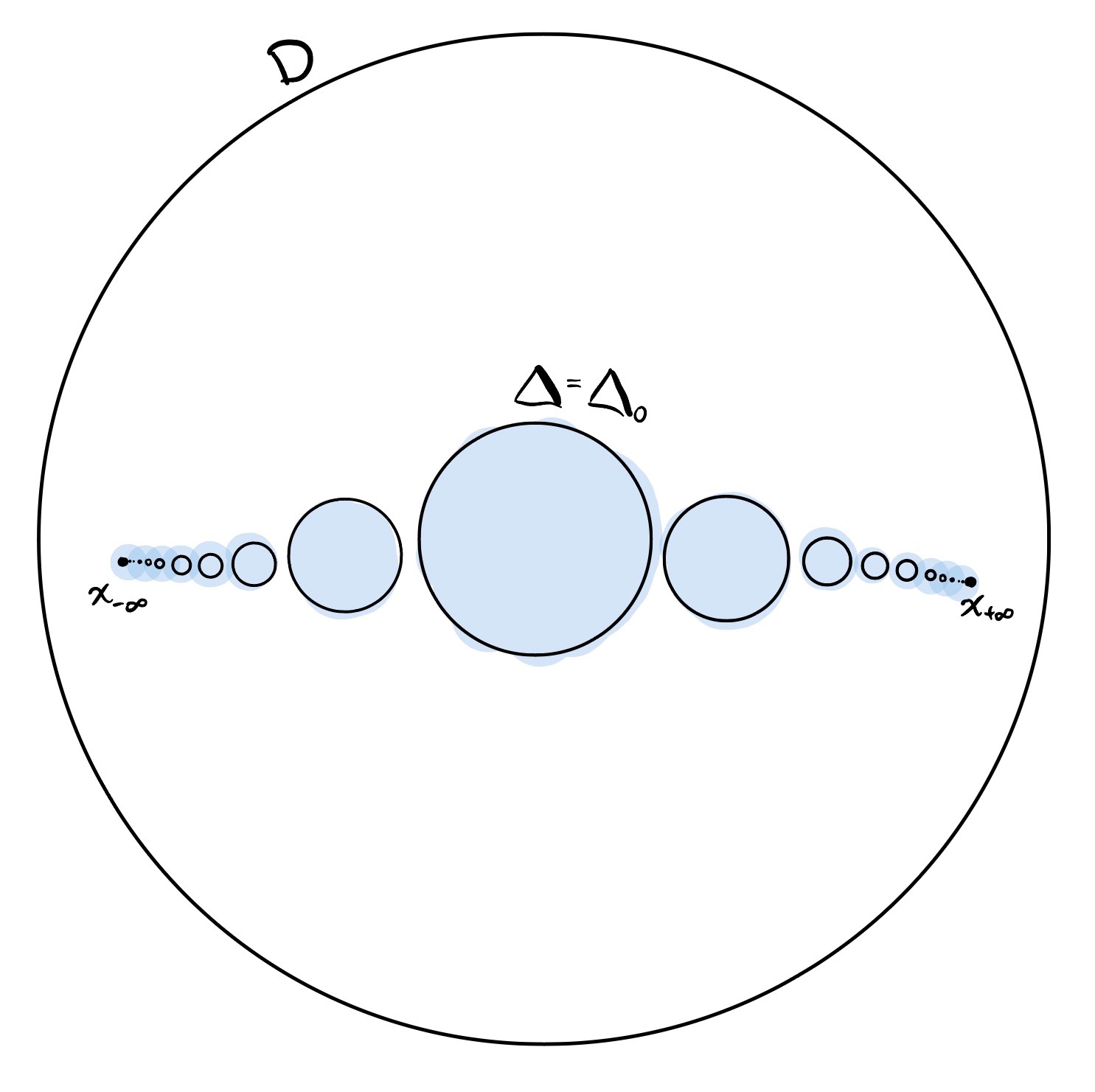
Here’s how we’ll use these disks. There is a homeomorphism $\varphi\colon D \to D$ which shifts each $\Delta_n$ to $\Delta_{n+1}$ and holds $x_{\pm\infty}$ fixed. Since the $\Delta_{n}$ are pairwise disjoint, if we choose distinct $n$ and $m$ , the homeomorphisms $\varphi^n g \varphi^{-n}$ and $\varphi^m g \varphi^{-m}$ have disjoint support and thus commute. Thus the infinite product $\sigma = \prod_{n = 0}^\infty \varphi^n g\varphi^{-n}$ makes sense as a homeomorphism whose support is contained in $D$ .
Proposition.
- $[\sigma,\varphi] = \sigma\varphi\sigma^{-1}\varphi^{-1} = g$ .
- Suppose $f$ is a homeomorphism of $S$ satisfying $f(D) \cap D = \varnothing$ and such that there exists a homeomorphism $\psi\colon S \to S$ exchanging $D$ and $f(D)$ and satisfying $\psi|_D = f$ and $\psi|_{f(D)} = \varphi f^{-1}$ . Then any normal subgroup of $\operatorname{Homeo}(S)$ containing $f$ contains $g$ .
Proof. From the definition of $\sigma$$ we have $ \varphi\sigma^{-1}\varphi^{-1} = \prod_{n=1}^\infty \varphi^n g^{-1} \varphi^{-n}$$ from which it follows that $\sigma(\varphi\sigma^{-1}\varphi^{-1}) = g$ . We claim that $g = [\sigma,f]\psi [\sigma,f]\psi^{-1}.$ Expanding, we see that this is a product of conjugates of $f$ and $f^{-1}$ and is thus contained in any normal subgroup containing $f.$
To see that this product is really $g$ , observe that since $\sigma$ is supported on $D$ , for $x \in D$ , we have $\sigma f \sigma^{-1}f^{-1}(x) = \sigma(x)$ . On the other hand, for $x \in f(D)$ , we have $\sigma f \sigma^{-1}f^{-1}(x) = \sigma^{-1}(x)$ . Thus if $x \in D$ ,
$$\psi\sigma f \sigma^{-1}f^{-1}\psi^{-1}(x) = \psi\sigma f \sigma^{-1} f^{-1} f\varphi^{-1}(x) = \psi f \sigma^{-1} \varphi^{-1}(x) = \varphi \sigma^{-1} \varphi^{-1}(x)$$
which is in $D$ , so further applying $\sigma f\sigma^{-1} f^{-1}$ we obtain $\sigma \varphi \sigma^{-1} \varphi^{-1}(x) = g(x)$ .
Next, if $x \in f(D)$ , we have $\psi^{-1}(x) = f^{-1}(x) \in D$ , applying $\psi [\sigma,f]$ yields $f \sigma f^{-1}(x),$ and further applying $\sigma f \sigma^{-1} f^{-1}$ yields $\sigma(x) = x$ , since $x \notin D$ .
Finally, if $x \notin D \cup f(D)$ , note that $f^{-1}\psi^{-1}(x)$ is not in $D$ , so we have $\psi[\sigma, f]\psi^{-1}(x) = x$ and in fact the whole product fixes $x$ . Thus we have shown that $g = [\sigma, f]\psi[\sigma,f]\psi^{-1}$ . $\blacksquare$
Simplicity of $\operatorname{Homeo}_+(S^2)$ .
Now, all of $\operatorname{Homeo}(S^2)$ cannot be simple, since it has an action on the $2$ -element set of orientations of $S_2$ . On the other hand, let’s show that $\operatorname{Homeo}_+(S^2)$ is simple. To do so, we want to apply the proposition, for which we need to express any given orientation-preserving homeomorphism $h\colon S^2 \to S^2$ as being built out of homeomorphisms supported on disks.
Suppose at first that $h$ fixes some (topological) circle on $S^2$ . Then $h$ is the product of $h^+$ and $h^-$ , which are supported in the two hemispheres (thanks Schoenflies!) determined by the circle. If $h$ does not fix a given circle $C$ , say one disjoint from some fixed point $p$ of $h$ , there is again a homeomorphism $h'$ of $S^2$ fixing $p$ taking $h(C)$ back to $C$ (thanks Schoenflies!) so that the composition $h'h$ fixes $C$ , and we can use the argument from above. It looks like this expresses $h$ as the product of three homeomorphisms supported in disks, but Nick observed that we can actually combine $h'$ with one of $h^+$ or $h^-$ , so only two are needed.
Anyway, now we have $h = h^+h^-$ where each of $h^+$ and $h^-$ are supported in disks $D^+$ and $D^-$ . If $f$ displaces $D^+$ (i.e. $f(D^+) \cap D^+ = \varnothing$ ) and $\iota_+^-$ is an orientation-preserving homeomorphism of $S^2$ taking $D^+$ to $D^-$ , (one exists! I think this is still thanks Schoenflies!) we have that $\iota_+^- f (\iota_+^-)^{-1} (D^-) \cap D^- = \varnothing$ . Indeed, if our original $f$ had a $\psi$ , then our new $\iota_+^- f (\iota_+^-)^{-1}$ has one.
It follows from the proposition, assuming we can construct $\psi$ , that $h^+$ and $h^-$ are both products of conjugates of $f$ , so so is $h$ . But now $f$ itself can be arbitrary so long as it’s nontrivial, for if $f(x) \ne x$ , we can find an open neighborhood small enough that it is moved entirely off itself, and this open neighborhood contains some disk that $f$ therefore displaces. Therefore the smallest normal subgroup of $\operatorname{Homeo}_+(S^2)$ containing a nontrivial element is the whole group—we’ve shown it is simple.
Other results
From here it’s actually not too hard to show that $\operatorname{Homeo}_+(S^2)$ is coarsely bounded. Originally I was going to give some argument here, but I have to turn in an application tomorrow, so I’ll sign off and work on that instead.