this is the eigth and final post in a series on Katie Mann and Kasra Rafi’s paper Large-scale geometry of big mapping class groups. The purpose of this post is to tie up a loose end. In the third post, we observed that if $\operatorname{Map}(\Sigma)$ is to be coarsely bounded, then any finite, $\operatorname{Map}(\Sigma)$ -invariant set of ends has cardinality at most two, but then went on to discuss the case of self-similarity, where such a set has cardinality one. I’d like to discuss that remaining case.

Suppose $\Sigma$ has coarsely bounded mapping class group. Then certainly it has locally coarsely bounded mapping class group, and is generated by a coarsely bounded set (the whole group) so by the fourth post, there is a decomposition of $\operatorname{Ends}(\Sigma)$ into finitely many self-similar pieces. By the argument in the third post, if we minimize the number of self-similar sets in the decomposition (i.e. don’t split up pieces with a Cantor set of ends of the same type into more than one self-similar set) then there are at most two self-similar pieces, since otherwise a finite-type subsurface realizing this decomposition would be nondisplaceable. Similarly the genus of $\Sigma$ is zero or infinite. If there were only one self-similar piece, then $\operatorname{Ends}(\Sigma)$ is self-similar, and we showed in the third post that $\operatorname{Map}(\Sigma)$ is coarsely bounded. So suppose there are two pieces, $A$ and $B$ . If one of these pieces, say $A$ , has a Cantor set of maximal ends, then a pair of pants dividing $A$ into two pieces and separating them from $B$ will be nondisplaceable. Therefore there are exactly two maximal ends $\xi$ and $\zeta$ , each with self-similar neighborhoods $A$ and $B$ respectively such that $\operatorname{Ends}(\Sigma) = A \sqcup B$ . This decomposition may be realized by cutting open $\Sigma$ along some separating simple closed curve $\alpha$ . Call the two complementary subsurfaces $\Sigma_A$ and $\Sigma_B$

Recall as well from the fourth post that we have “shift” homeomorphisms $f_{\Sigma_\xi}$ satisfying, for any subsurface $\Sigma_\xi$ of $\Sigma$ with one boundary component containing $\xi$ in its end set, $f_{\Sigma_\xi}(\Sigma_\xi) \supset \Sigma_A$ . This implies that either both $\xi$ and $\zeta$ are planar (and thus $\Sigma$ has genus zero) or both nonplanar.

Let us argue that $\operatorname{Ends}(\Sigma)$ is uncountable. If it were countable, then $\operatorname{Ends}(\Sigma)$ would be homeomorphic to $\omega^\alpha \cdot 2 + 1$ , where $\alpha$ is a successor ordinal (otherwise $\Sigma$ would have limit type) and the subset of nonplanar ends is some closed subset containing both the maximal ends. We can think of $\Sigma$ as sort of a two-sided flute of some kind, possibly with genus going off to both ends. In particular, there is a countable collection of pre-maximal ends, all pairwise homeomorphic and limiting to $\xi$ and $\zeta$ . The construction in the sixth post produces a continuous homomorphism from the pointwise stabilizer of $\xi$ and $\zeta$ (which has index two in $\operatorname{Map}(\Sigma)$ ) to $\mathbb{Z}$ . This is a contradiction, because $\mathbb{Z}$ is not coarsely bounded.

Telescoping

It turns out that when $\Sigma$ is tame, the assumption that $\operatorname{Map}(\Sigma)$ is coarsely bounded implies that $\Sigma$ is what is called telescoping, a term which we now define. We say that $\Sigma$ is telescoping with respect to a pair of ends $\xi$ and $\zeta$ if there exist disjoint subsurfaces $\Sigma_\xi$ and $\Sigma_\zeta$ each with one boundary component and having $\xi$ and $\zeta$ as ends, respectively, with the property that for any smaller subsurfaces $\Sigma'_\xi \subset \Sigma_\xi$ and $\Sigma'_\zeta \subset \Sigma_\zeta$ (also with one boundary component and containing $\xi$ or $\zeta$ as an end respectively) there exist four homeomorphisms $f_\xi$ , $f_\zeta$ , $h_\xi$ and $h_\zeta$ with the following properties:

and

For example, consider the surface $\Sigma$ which has a Cantor set of ends accumulated by genus and a Cantor set of other ends which ends the nonplanar ends in two points. The surface $\Sigma$ looks something like this.

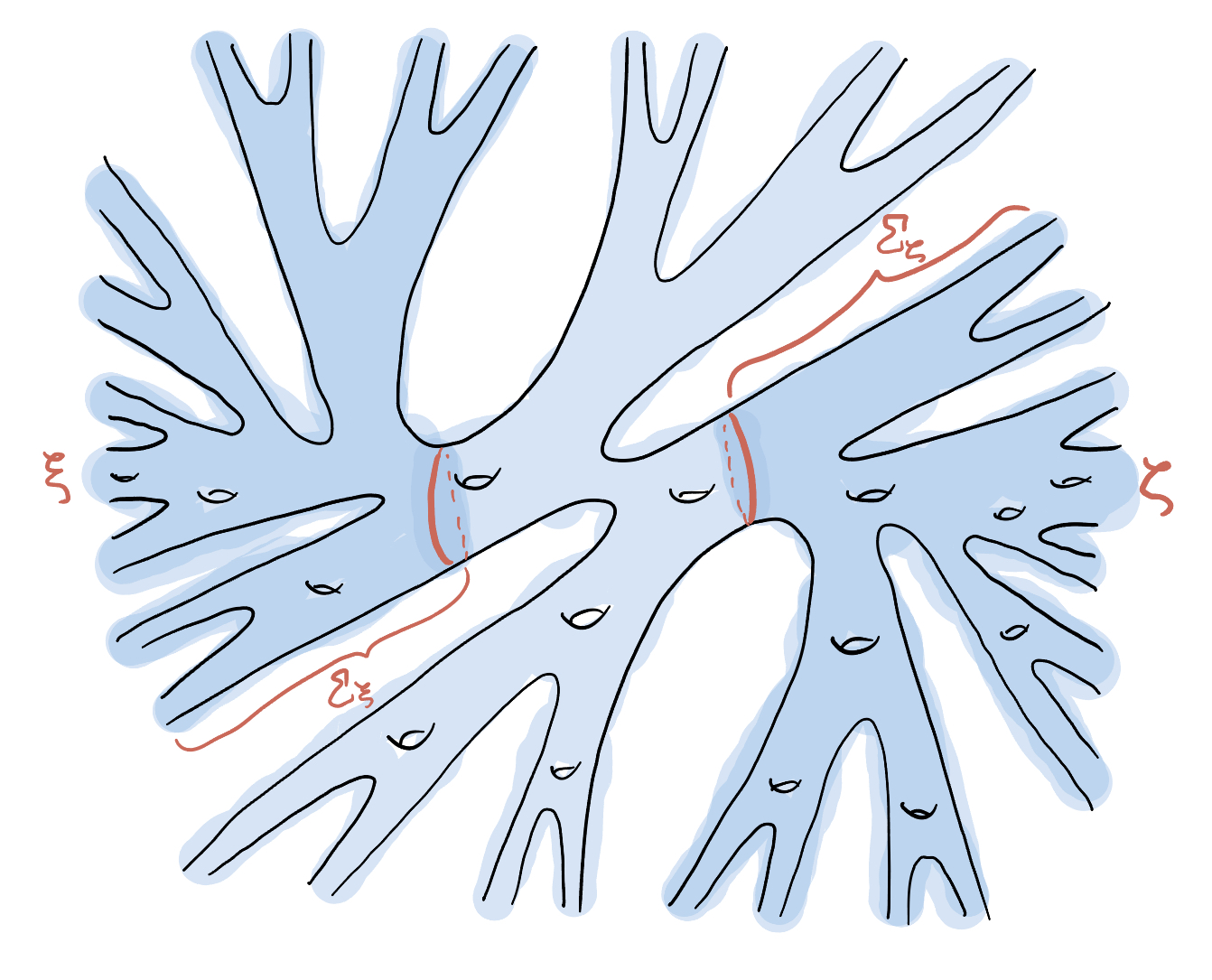
The ends $\xi$ and $\zeta$ are horizontally left and right, being the place where the ends accumulated by genus (bottom) and the planar ends (top) meet. For the subsurfaces $\Sigma_\xi$ and $\Sigma_\zeta$ there is a lot of freedom of choice; the main constraint is that the complement of $\Sigma_\xi \cup \Sigma_\zeta$ should have a Cantor set each of planar and nonplanar ends. It may be instructive to choose the smaller subsurfaces and attempt to construct the four required homeomorphisms.

Anyway, we have the following pair of results. The proof of the latter is analogous to the argument in the third post; it might be worthwhile attempting it as an exercise on the example surface $\Sigma$ .

Theorem 1.6 (Mann–Rafi). Supposing $\Sigma$ is tame, then $\operatorname{Map}(\Sigma)$ is coarsely bounded if and only if $\Sigma$ has infinite or zero genus and either $\operatorname{Ends}(\Sigma)$ is self-similar or $\Sigma$ is telescoping.

Proposition 3.5 (Mann–Rafi). If $\Sigma$ is telescoping with respect to ends $\xi$ and $\zeta$ , then the pointwise stabilizer of $\xi$ and $\zeta$ is coarsely bounded in $\operatorname{Map}(\Sigma)$ . In particular, if $\xi$ and $\zeta$ are the unique pair of maximal ends of $\Sigma$ , then $\operatorname{Map}(\Sigma)$ is coarsely bounded.