Rylee Alanza Lyman

This post is, strictly speaking, a follow up to part three of my series on stacks, on the 2-Yoneda lemma. The classical Yoneda lemma has built into it a naturality statement, while our 2-Yoneda lemma proved essentially only the fact of the isomorphism. Let’s fix that.

Theorem. (The 2-Yoneda Lemma) The functor $\operatorname{よ}\colon \operatorname{Hom}(\underline{X},\mathsf{D}) \to \mathsf{D}(X)$ defined on objects as $(F\colon \underline{X} \to \mathsf{D}) \mapsto F(1_X)$ and on arrows as $(\alpha\colon F \Rightarrow G) \mapsto \alpha(1_X)$ is an equivalence of categories which is pseudonatural in both arguments.

We have proved all but the (pseudo)-naturality statement, which is a little convoluted for the following reason. You see, typically you think of the Yoneda lemma as being about, for instance, natural transformations from the hom-set functor $\mathsf{C}(\underline{X},\cdot)$ to a functor $F$ . Now, $\underline{X}$ is not the functor $\mathbf{Top}(X,\cdot)$ , but rather the functor $\mathbf{Top}(\cdot,X)$ which we think of as being valued not in sets, but in categories (groupoids, actually), where the category is the rather uninteresting discrete category comprising an object for each map $Y \to X$ and only the identity arrows. Given a map $h \colon Y \to Z$ , we get a functor $h^*\colon \underline{X}(Z) \to \underline{X}(Y)$ given by $h^*(g\colon Z \to X) = gh \colon Y \to X$ . This is actually a functor (I say, just because I can anticipate that I’m about to write down a not-quite-a-functor). The only natural transformation between functors is the identity.

Anyway, the point is, we should be expecting to suddenly start thinking of an arbitrary category fibered in groupoids $\mathsf{D}$ as a contravariant functor from $\mathsf{Top}$ to the category of categories (groupoids, actually), where the category is $\mathsf{D}(Y)$ . Given a map $h \colon Y \to Z$ , we should get a functor $h^*\colon \mathsf{D}(Z) \to \mathsf{D}(Y)$ given by $h^*(\xi) = h^*\xi$ and we do, actually. The problem, which we mumbled something about earlier, is that given $g \colon X \to Y$ , we don’t necessarily have $g^*h^*\xi = (hg)^*\xi$ , merely that they’re canonically isomorphic. In other words, the operation $(\cdot)^*$ is not a contravariant functor, just one up to canonical isomorphism. I super don’t actually want to learn what a pseudofunctor is, but I guess that’s what this is.

A digression: pseudofunctors

Let’s go slowly: for each object $X$ in $\mathbf{Top}$ we have an object in the category of groupoids, namely the groupoid $\mathsf{D}(X)$ . If we think of the hom-set $\mathbf{Top}(X,Y)$ as a discrete groupoid, we get a covariant functor defined contravariantly on objects (which are maps!) as $(f\colon X\to Y) \mapsto f^*\colon \mathsf{D}(Y) \to \mathsf{D}(X)$ . We saw that this is in fact a functor, since given $\alpha \colon \xi \to \xi'$ , there is a unique arrow $f^*\alpha \colon f^*\xi \to f^*\xi'$ . The arrows of the category $\mathbf{Top}(X,Y)$ are the identity natural isomorphism, which must go to the identity natural transformation of $f^*$ . Now, I think we’ve insisted that $1_X^*\xi = \xi$ , and indeed if you pull back a bundle along the identity map, I think it’s fair to say that you get the same bundle. This is secretly good, because it lets us ignore isomorphisms involving the identity, since they are equalities. Now for the hard part. Given $f\colon X \to Y$ and $g \colon Y \to Z$ , by the defining property of a category fibered in groupoids, for each $\xi \in \mathsf{D}(Z)$ , there is a unique isomorphism $\eta{f,g}(\xi)$ making the following diagram commute

Notice that given an arrow $\alpha\colon \xi \to \xi'$ , the following diagram commutes

This is because of the defining property of categories fibered in groupoids: both paths around the square make the following diagram commute

indeed we calculate

and

My source (nLab, gulp) suggests that the isomorphism $\eta_{f,g}$ should be natural in $f$ and $g$ . Notice that if $f \ne f'$ , then there are no natural transformations (isomorphisms) $f^* \Rightarrow f'^*$ . On the other hand, a family of arrows $\alpha(\xi) \colon f^*\xi \to f^*\xi$ , define a natural isomorphism $\alpha \colon f^*\Rightarrow f^*$ if for each $\beta \colon \xi \to \xi'$ in the fiber over $\mathsf{Y}$ , we have $\alpha(\xi')f^*\beta = f^*\beta\alpha(\xi)$ . Naturality in $f$ , then, is the statement that given $\alpha\colon f^* \Rightarrow f^*$ , the following diagram commutes

which can only hold if the righthand arrow is $\eta_{f,g}(\xi)\alpha(g^*\xi)\eta_{f,g}(\xi)^{-1}$ , and indeed, I see no other sensible way to define an arrow $(gf)^*\xi \to (gf)^*\xi$ out of one from $f^*\xi \to f^*\xi$ . Naturality in $g$ should be similarly silly; I’ll leave it to you.

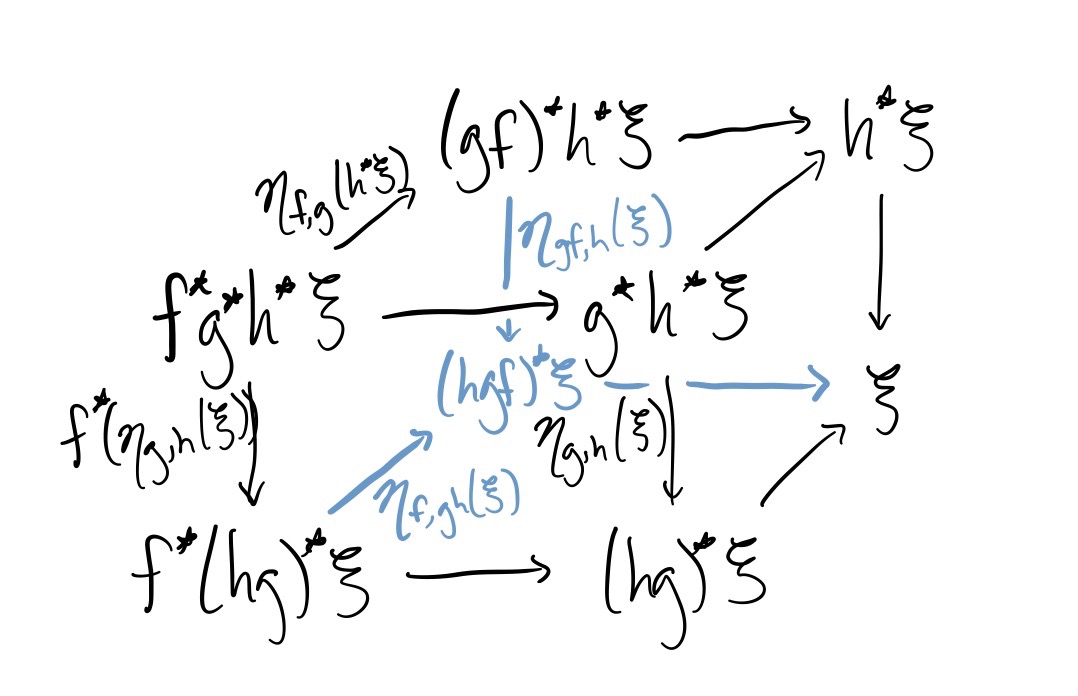
Since function composition is strictly associative (phew) we just need to check that the following diagram commutes for each $\xi \in \mathsf{D}(W)$ and each triple of maps $f\colon X \to Y$ , $g\colon Y \to Z$ and $h\colon Z \to W$

This will use our only trick: consider the diagram

We calculate:

and

Therefore by the defining property of categories fibered in groupoids, we have the coherence of the associating isomorphism. The argument above is summarized in the commuting cube below, where the unlabeled arrows are the “obvious” ones, for instance $h_\xi \colon h^*\xi \to \xi$ .

Pseudonaturality in $\underline{X}$

Okay enough about pseudofunctors. We already saw in a previous post that functors $\underline{Y} \to \underline{X}$ are maps $f\colon Y \to X$ . (Indeed, the proof uses the first part of the 2-Yoneda lemma.) Such a functor gives us a functor

defined on objects (functors) as $f^*F = Ff$ and on arrows (natural transformations) as $f^*(\alpha \colon F \Rightarrow G) = \alpha f \colon Ff \Rightarrow Gf$ . On the other side of the equation, we have the functor $f^*\colon \mathsf{D}(X) \to \mathsf{D}(Y)$ defined extensively above. Pseudonaturality in $X$ then is the claim that the following diagram commutes

up to a natural transformation. And indeed, if $F(1_X) = \xi \in \mathsf{D}(X)$ , we have $f^*\operatorname{よ}_X(F) = f^*\xi$ and $\operatorname{よ}_Y(f^*F) = (f^*F)(1_Y) = F(f\colon Y \to X)$ . Now, recall from part three that we write $F(Y)$ , since $f\colon Y \to X$ is understood and we’d like to consider the arrow $F(f) \colon F(Y) \to \xi$ . By the definition of categories fibered in groupoids, there is a unique isomorphism $\sigma_{F,f}\colon F(Y) \to f^*\xi$ satisfying $f_\xi \sigma_{F,f} = F(f)$ . We claim that $\sigma_{F,f}$ defines a natural transformation making the diagram above commute. This is the claim that for every natural transformation $\alpha\colon F\Rightarrow G$ in $\operatorname{Hom}(\underline{X},\mathsf{D})$ , the following diagram commutes in $\mathsf{D}(Y)$ :

Unwound slightly, if we write $G(X) = \xi'$ and $\alpha \colon \xi \to \xi'$ , this is the same diagram as

The commutativity of this diagram uses our only trick, namely the unique way of filling this diagram:

We check

$\alpha F(f) = \alpha f_\xi \sigma_{F,f} = f_{\xi'} f^*\alpha \sigma_{F,f}$

and

$\alpha F(f) = G(f)\alpha(Y) = f_{\xi'} \sigma_{G,f} \alpha(Y).$

A loose end from part six

I think this proves a claim from part six. Let’s test it out. An object $\xi \in \mathsf{D}(Y)$ is a map $f\colon \underline{Y} \to \mathsf{D}$ . Similarly $\xi' \in \mathsf{D}(X)$ is a map $g\colon \underline{X} \to \mathsf{D}$ . An arrow $\tilde h \colon \xi \to \xi'$ over a map $h\colon Y \to X$ should be the map $h \colon Y \to X$ together with a natural transformation $\alpha\colon f \Rightarrow gh$ .

Let me write things a little more like the above. So we have $\xi \in \mathsf{D}(Y)$ equal under $\operatorname{よ}_Y$ to $F\colon \underline{Y} \to \mathsf{D}$ , and similarly $\xi' = \operatorname{よ}_X(G)$ . We have the functor $\mathsf{D}(h) = h^*\colon \mathsf{D}(X) \to \mathsf{D}(Y)$ which corresponds up to natural transformation to precomposition by $h\colon Y \to X$ . There is a unique isomorphism $\beta$ making the following diagram commute

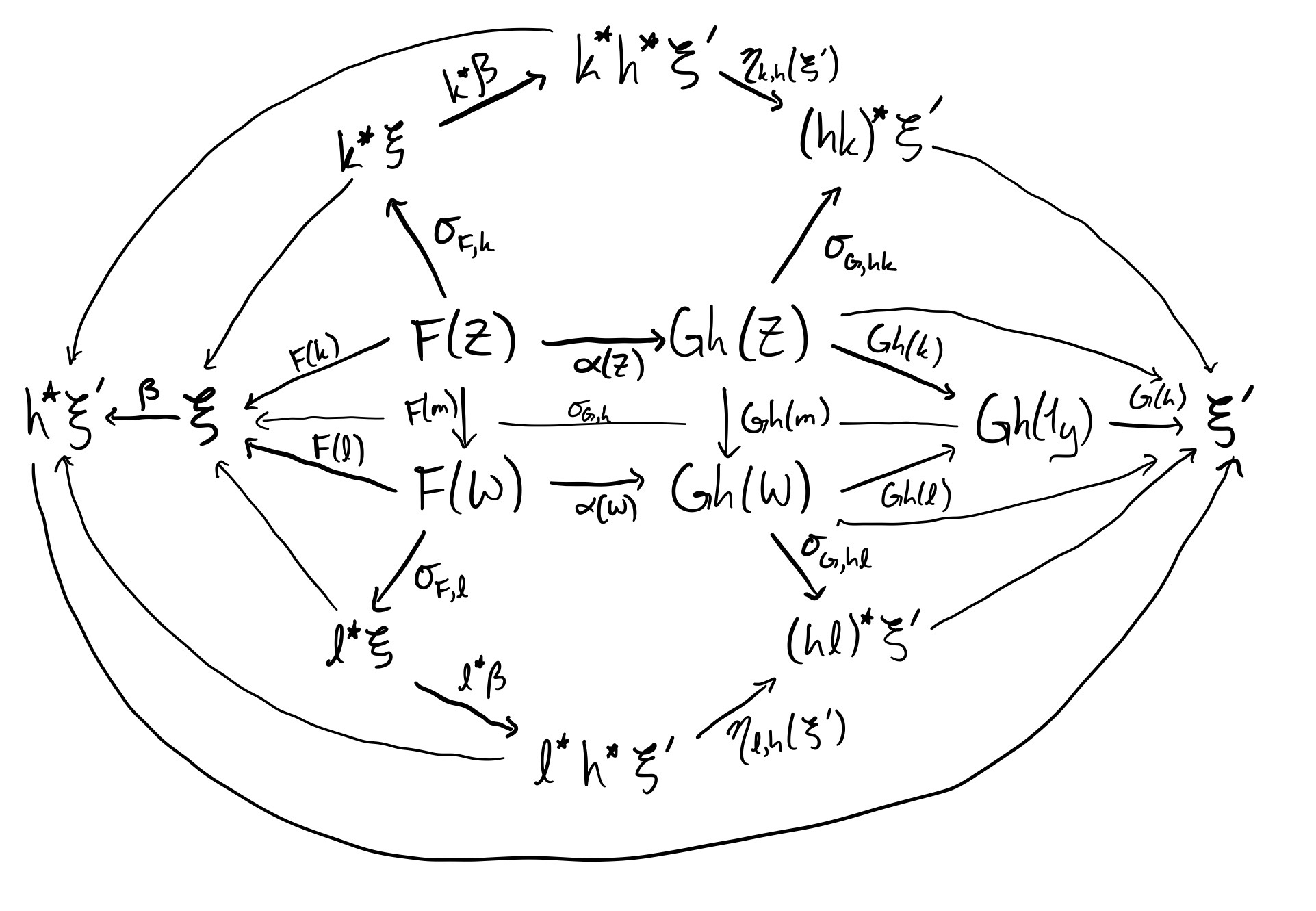
We claim that $\sigma_{G,h}^{-1}\beta$ comes from (or defines) a unique natural transformation $\alpha \colon F \Rightarrow Gh$ (we write $Gh$ to avoid confusion with the functor $h^*$ ). At an object $k \colon Z \to Y$ of $\underline{Y}$ , define $\alpha(Z) = \sigma_{G,hk}^{-1} \eta_{k,h}(\xi') k^*\beta \sigma_{F,k}$ , where $\eta_{k,h}(\xi') \colon k^*h^*\xi' \to (hk)^*\xi'$ is the isomorphism defined in the previous section. Given another object $\ell \colon W \to Y$ and an arrow $m \colon Z \to W$ , we need the following diagram to commute

Let’s try putting both paths around the square into the diagram

We calculate

and

The argument is summarized in the following interesting commutative diagram.

Conversely it is clear that given such an $\alpha \colon F \Rightarrow Gh$ , we get a map $\tilde h \colon \xi \to \xi'$ defined by $G(h)\alpha(Y)$ .

Pseudonaturality in $\mathsf{D}$

Now suppose we have a map of categories fibered in groupoids $f\colon \mathsf{C} \to \mathsf{D}$ . This is by definition a functor $f\colon \mathsf{C} \to \mathsf{D}$ such that $\pi f = \pi$ . For each $\xi \in \mathsf{C}(X)$ , we get an object $f(\xi) \in \mathsf{D}(X)$ , and for each arrow $\alpha \colon \xi \to \xi'$ in the fiber, we get an arrow $f(\alpha)\colon f(\xi) \to f(\xi')$ in the fiber. In other words, we get a functor $f|_X \colon \mathsf{C}(X) \to \mathsf{D}(X)$ . Given a functor $F\colon \underline{X} \to \mathsf{C}$ , postcomposition with $f$ yields a functor $f_*F = fF \colon \underline{X} \to \mathsf{D}$ . Similarly given a natural transformation $\alpha\colon F\Rightarrow G$ , we get $f_*\alpha \colon f_*F\Rightarrow f_*G$ . Pseudonaturality in $\mathsf{D}$ is the claim that the following diagram commutes

up to a natural transformation. And indeed, if we write $F(1_X) = \xi$ , $G(1_X) = \xi'$ and $\alpha(1_X) = \alpha \colon \xi \to \xi'$ , we actually have

and

so the diagram actually commutes on the nose.