Okay, we’re closing in on the definition of a geometric stack over $\mathbf{Top}$ . Actually, the nLab tells me such stacks are called topological, so I’ll try and say that. But! Before we get there, we need the construction of the 2-fiber product of categories fibered in groupoids over $\mathbf{Top}$ . The purpose of this post is to discuss this construction, which I think is adorable. I cannot shake the feeling that I’ve talked through the 2-fiber product of categories before, but I have no idea where or why I might have done this except possibly the last time I tried to learn about stacks.
Friends of the blog will recall the categorical definition of a pullback. This notion makes sense for categories (after all, categories assemble into a category), but because of the existence of natural transformations, the universal property looks a little bit different. Namely, suppose we have three categories $\mathsf{C}$ , $\mathsf{D}$ and $\mathsf{E}$ and two functors $F\colon \mathsf{C} \to \mathsf{E}$ and $G\colon \mathsf{D} \to \mathsf{E}$ . The 2-fiber product $\mathsf{C}\times_{\mathsf{E}} \mathsf{D}$ makes the following diagram commute
up to natural isomorphism $\eta\colon F\pi_1 \Rightarrow G\pi_2$ and is universal for this property in the following slightly complicated sense. Given any category $\mathsf{X}$ , maps $H\colon \mathsf{X} \to \mathsf{C}$ and $K\colon \mathsf{X} \to \mathsf{D}$ with a natural isomorphism $\epsilon \colon FH \Rightarrow GK$ , there is a functor $P\colon\mathsf{X} \to \mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ and natural isomorphisms $\alpha\colon H \Rightarrow \pi_1P$ and $\beta\colon K\Rightarrow \pi_2P$ with the property that $(G\beta)^{-1} \circ \eta P \circ F\alpha = \epsilon$ . This is summarized in the following diagram.
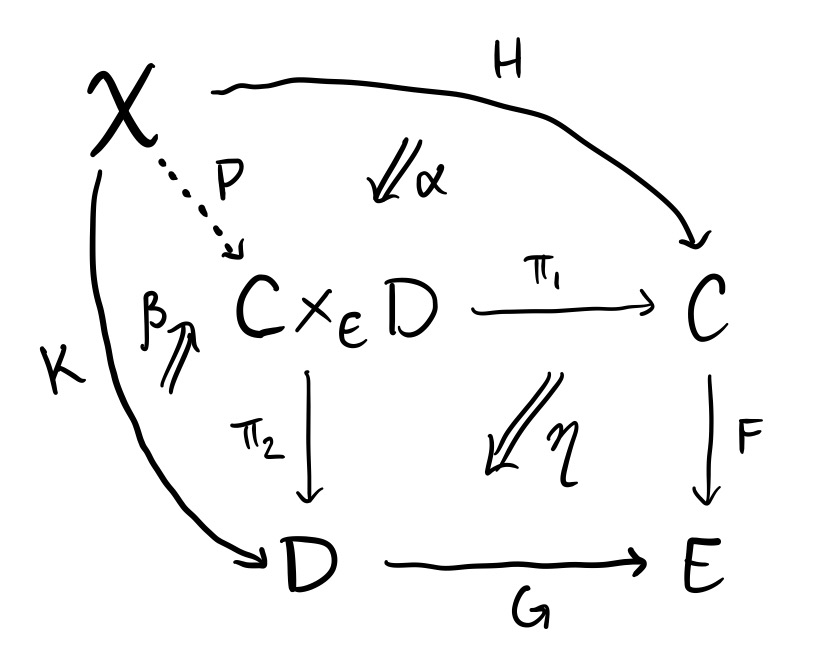
Given another functor $Q\colon \mathsf{X} \to \mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ and natural isomorphisms $\gamma\colon H\Rightarrow \pi_1Q$ and $\delta\colon K \Rightarrow \pi_2Q$ as above, there exists a unique natural isomorphism $\lambda \colon P \Rightarrow Q$ with the property that $\pi_1\lambda \colon \pi_1P \Rightarrow \pi_1Q$ equals $\gamma\circ\alpha^{-1}$ and $\pi_2\lambda = \delta\circ\beta^{-1}$ .
In the case of categories fibered in groupoids over $\mathbf{Top}$ , the 2-fiber product has the following definition. Objects of $\mathsf{C}\times_{\mathsf{E}} \mathsf{D}$ are triples $(c,d,\alpha)$ , where $c \in \mathsf{C}$ and $d \in \mathsf{D}$ are objects over the same space $X$ and $\alpha\colon F(c) \to G(d)$ is an arrow over the identity map of $X$ . Arrows of $\mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ are pairs of arrows $u\colon c_1 \to c_2$ and $v\colon d_1 \to d_2$ over the same map of spaces $f\colon X \to Y$ with the property that the following diagram commutes in $\mathsf{E}$
There is an obvious functor $\pi\colon \mathsf{C}\times_{\mathsf{E}}\mathsf{D} \to \mathbf{Top}$ sending an object $(c,d,\alpha)$ to the space $X$ that $c$ and $d$ are over and sending an arrow $(u,v)$ to the map $f\colon X \to Y$ that $u$ and $v$ are over. We’d like to show that $\mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ is fibered in groupoids. Given an object $\xi = (c,d,\alpha)$ over $X$ and a map $f\colon Y \to X$ , we need a “pullback” $f^*\xi$ over $Y$ . It would be simplest to define $f^*\xi = (f^*c,f^*d,f^*\alpha)$ , but we don’t necessarily have $f^*F(c) = F(f^*c)$ , merely that they are canonically isomorphic via an isomorphism $\sigma_{F,f}\colon F(f^*c) \to f^*F(c)$ such that $F(f_c) = f_{F(c)} \sigma_{F,f}$ . So we will in fact define $f^\xi = (f^*c, f^*d, \sigma_{G,f}^{-1} f^*\alpha \sigma_{F,f})$ . The map $f_\xi \colon f^*\xi \to \xi$ is the map $(f_c,f_d)$ . We check
so this really does give a map $f_\xi \colon f^*\xi \to \xi$ .
Given a pair of arrows $(u_1,v_1)\colon (c_1,d_1,\alpha_1) \to (c,d,\alpha)$ and $(u_2,v_2)\colon (c_2,d_2,\alpha_2) \to (c,d,\alpha)$ over maps $f \colon Y \to X$ and $g\colon Z \to X$ such that there exists a map of spaces $h\colon Y \to Z$ with $gh = f$ , we need a unique pair of maps $h_{\mathsf{C}}\colon c_1 \to c_2$ and $h_{\mathsf{D}}\colon d_1 \to d_2$ such that the relevant diagram commutes. But observe that because $u_1$ and $u_2$ are over $f$ and $g$ , there does exist a unique map $h_{\mathsf{C}}\colon c_1 \to c_2$ and similarly a unique map $h_{\mathsf{D}}\colon d_1 \to d_2$ lifting the diagram $gh = f$ . We need to check that the following diagram commutes
We will show this by the strategy from the last post: fitting both paths around the square into the vertical arrow in the following diagram
uniqueness then assures equality of the paths around the square. We have
$\alpha F(u_1) = G(v_1)\alpha_1 = G(v_2)G(h_{\mathsf{D}})\alpha_1.$On the other hand we have
$\alpha F(u_1) = \alpha F(u_2)F(h_{\mathsf{C}}) = G(v_2) \alpha_2 F(h_{\mathsf{C}}),$how satisfying! This shows that the 2-fiber product really is fibered in groupoids.
On the other hand, we have obvious projections $\mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ to $\mathsf{C}$ and $\mathsf{D}$ . Call these $\pi_1$ and $\pi_2$ . We do not quite have $F\pi_1 = G\pi_2$ , merely that there is a natural isomorphism $\eta\colon F\pi_1 \Rightarrow G\pi_2$ defined by $\eta(c,d,\alpha) = \alpha$ ! Adorable, right? Showing that $\eta$ really is natural is cute, but I’ll leave it to you.
By the way, are you still thinking vector bundles? I know I am; it’s helpful to pretend that there really is a projection from $\xi \in \mathsf{C}$ down to the space $X$ it is over.
The universal property
I’d like to conclude this post by showing that the fiber product really has its universal property. Given a category $\mathsf{X}$ fibered in groupoids over $\mathbf{Top}$ with functors $H \colon \mathsf{X} \to \mathsf{C}$ and $K\colon \mathsf{X} \to \mathsf{D}$ and a natural isomorphism $\epsilon\colon FH \Rightarrow GK$ , the obvious functor $P$ to $\mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ is defined on objects as $x \mapsto (H(x),K(x),\epsilon(x))$ and on arrows $(u\colon x \to y) \mapsto (H(u),K(u))$ . Naturality of $\epsilon$ assures that this is really a functor. In this case, the isomorphisms $\alpha\colon H \Rightarrow \pi_1P$ and $\beta\colon K \Rightarrow \pi_2P$ are the identity: these diagrams commute on the nose. Now suppose we have another functor $Q\colon \mathsf{X} \to \mathsf{C}\times_{\mathsf{E}}\mathsf{D}$ and natural isomorphisms $\gamma \colon H \Rightarrow \pi_1Q$ and $\delta\colon K \Rightarrow \pi_2Q$ . Define $\lambda \colon P \Rightarrow Q$ by the rule $\lambda(x) = (\gamma(x),\delta(x))\colon (H(x),K(x),\epsilon(x)) \to Q(x)$ . We write $Q(x) = (c,d,\alpha)$ . We need the following diagram to commute
But this is exactly the condition at $x$ for the equality $(G\delta)^{-1}\eta Q F\gamma = \epsilon$ , so $\lambda(x)$ really defines an arrow. Given an arrow $u\colon x \to y$ in $\mathsf{X}$ , we need to check naturality:
This is true in each factor, for example in $\mathsf{C}$ we have $\pi_1 Q(u) \gamma(x) = \gamma(y) H(u)$ . Therefore both paths around the square give equal arrows. It is clear from the construction that $\lambda$ is unique.