This is the sixth post in a series on Katie Mann and Kasra Rafi’s paper Large-scale geometry of big mapping class groups. The purpose of this post is to discuss when a Polish group is generated by a coarsely bounded set, and give examples of mapping class groups which are locally coarsely bounded but fail this criterion.
The general case
We have the following theorem of Rosendal.
Theorem 1.2 (Rosendal). Let $G$ be a Polish group. Then $G$ is generated by a coarsely bounded set if and only if $G$ is locally coarsely bounded and not the countably infinite union of a chain of proper, open subgroups.
Let’s make sense of this. Note that countable, discrete groups are Polish. Being generated by a coarsely bounded set is the analogue of finite generation for discrete groups, so we should expect that for a countable discrete group (which is automatically locally coarsely bounded, having finite discrete neighborhoods of the identity) being finitely generated is equivalent to not being the countably infinite union of a chain of proper subgroups, which are automatically open.
Indeed, suppose $G$ is finitely generated by a set $S$ , and that $G_1 < G_2 < G_3 < \cdots$ is a strictly increasing chain of proper subgroups. Since the union of the $G_i$ is $G$ , each $s \in S$ belongs to some $G_i$ , but then at some finite stage $G_n$ , we have each $s \in S$ contained in $G_n$ , so actually $G_n = G$ .
Conversely, supposing every strictly increasing chain of proper subgroups terminates, we show that $G$ is finitely generated. Indeed, we can take a sequence of finitely generated subgroups! Begin with $G_1 = \langle s_1 \rangle$ for some $s_1 \in G$ . At each stage, add $s_{n+1} \notin G_n$ and take $G_{n+1} = \langle s_1,\ldots,s_{n+1}\rangle$ . Since this sequence terminates, we’ve proven that $G$ is finitely generated. (This proof contains the useful fact that every generating set for a finitely generated group contains a \emph{finite} generating set.)
A non-example: limit type
Remember the “Great Wave off Kanagawa” surface from the previous post? It had genus zero and end space homeomorphic to $\omega^\omega + 1$ in the order topology. Take the connect sum of two copies of that surface; so the genus-zero surface with end space homeomorphic to $\omega^\omega \cdot 2 + 1$ . It looks a little like this:
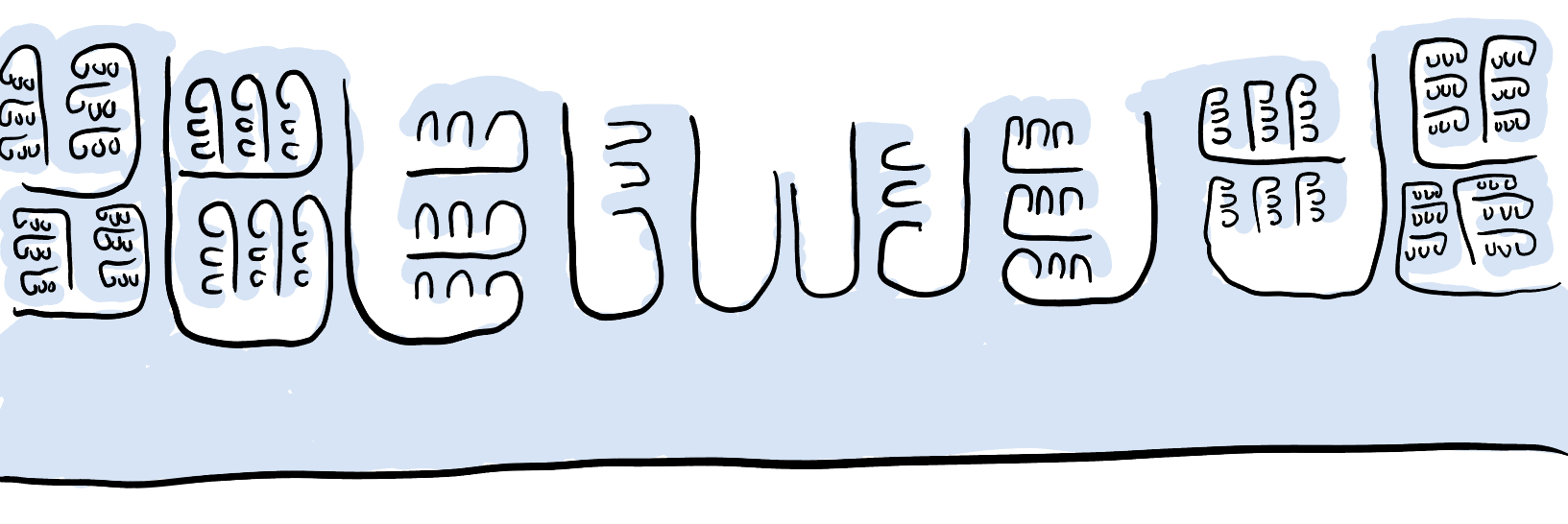
The original “Great Wave” surface has self-similar end space and genus zero, so has coarsely bounded mapping class group. This surface $\Sigma$ has locally coarsely bounded mapping class group, but we will show that $\operatorname{Map}(\Sigma)$ is not generated by a coarsely bounded set. Consider the index-two subgroup $G$ of $\operatorname{Map}(\Sigma)$ comprising those mapping classes that fix pointwise the two maximal ends. We’ll show that $G$ is a countable union of proper open subgroups $G_0 < G_1 < \cdots$ . Since $G$ has index two in $\operatorname{Map}(\Sigma)$ , this will show that $\operatorname{Map}(\Sigma)$ is also a countable union of proper open subgroups $G'_0 < G'_1 < \cdots$ , where each $G'_i$ is obtained from $G_i$ by adding a fixed mapping class $\phi$ that swaps the two maximal ends of $\Sigma$ . (Recall that a subgroup is open if and only if it contains an open neighborhood of the identity, so the $G'_i$ are open since $G$ is open in $\operatorname{Map}(\Sigma)$ and the $G'_i$ are open in $G$ .)
To start, consider a simple closed curve $\alpha$ separating $\Sigma$ into two pieces, each containing exactly one maximal end. The identity neighborhood we consider is $U_A$ , where $A$ is an annular subsurface with core curve $\alpha$ . Since $U_A$ is a subgroup of $G$ , we’ll let $G_0 = U_A$ . Since $\operatorname{Map}(\Sigma)$ and hence $G$ is Polish, there is a countable dense subset $\{\phi_i : i \in \mathbb{N}\}$ of $G$ . Any open subgroup containing the $\phi_i$ is in fact all of $G$ , so consider the sequence of open subgroups $G_1 \le G_2 \le \cdots$ , where
$G_i = \langle G_0, \phi_1,\ldots, \phi_i \rangle.$If we can show that each $G_i$ is a proper subgroup of $G$ , we will be done, even though a priori this chain may not be strictly increasing. Consider a maximal end $\xi$ and a neighborhood basis of $\xi$ comprising nested clopen neighborhoods $U_j$ with $U_{j+1} \subset U_j$ , beginning with $U_0$ being the end set of the component of $\Sigma - A$ containing $\xi$ . In the figure we can think of the clopen neighborhoods as coming from the “fluting” process described in the previous post. Thus, $U_0 - U_j$ contains points homeomorphic to $\omega^{j-1} + 1$ but not points homeomorphic to $\omega^j + 1$ . In plainer words, $U_0 - U_1$ contains isolated planar ends, $U_0 - U_2$ contains ends accumulated by isolated planar ends, $U_0 - U_3$ contains ends accumulated by ends accumulated by isolated planar ends, so on and so forth.
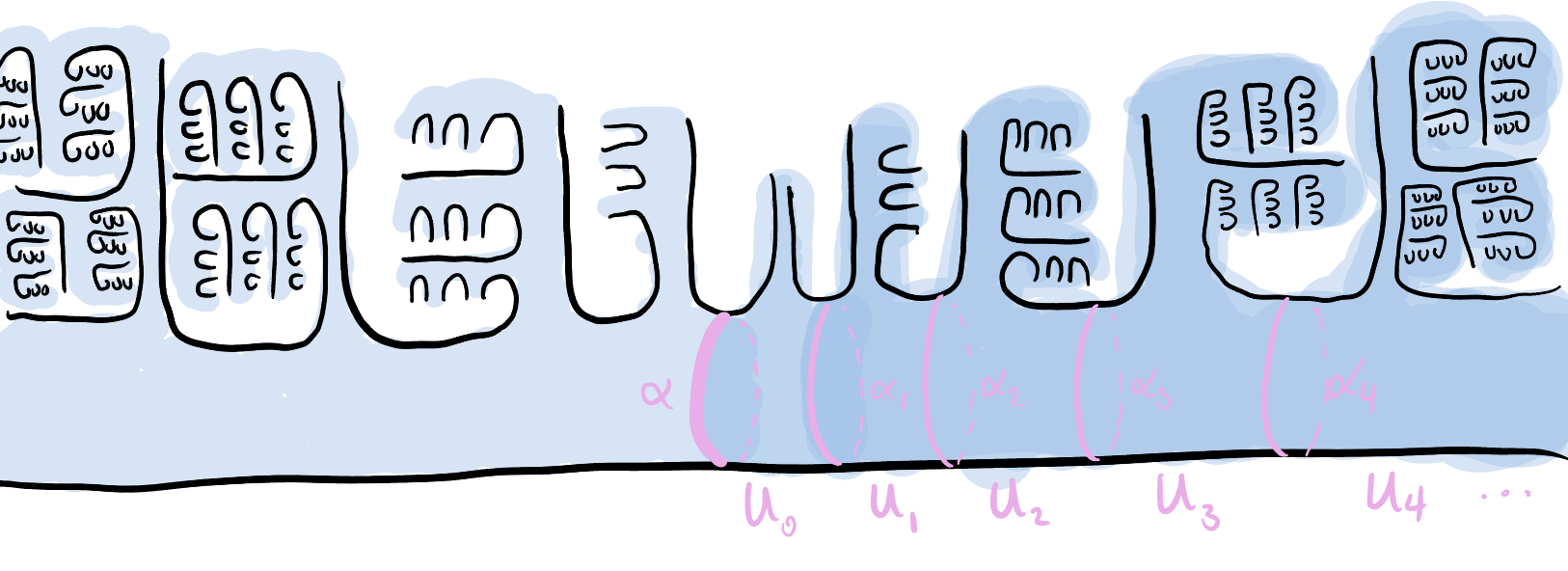
Anyway, consider $\phi_1,\ldots,\phi_n$ . Since each $\phi_i$ leaves $\xi$ invariant, we claim that there exists $M$ large such that for all $m \ge M$ , ends homeomorphic to $\omega^m + 1$ contained in $U_m$ actually remain inside $U_m$ under each $\phi_i$ . To see this, note that if there was a sequence of ends $\{\xi_m\}$ with each $\xi_m$ homeomorphic to $\omega^m + 1$ such that each $\xi_m$ was moved outside of $U_m$ by some $\phi_i$ , then since the sequence $\{\xi_m\}$ necessarily converges to $\xi$ , by the pigeonhole principle some $\phi_i$ would have to move $\xi$ . This already shows us that $G_i$ is a proper subgroup of $G$ , since by the classification of surfaces we can move some $\xi_m$ with $m > M$ outside of $U_m$ (and into a neighborhood of the other maximal end).
This surface $\Sigma$ is an example of the general phenomenon Mann–Rafi term having end space of “limit type”. The argument we just gave generalizes to show that if $\Sigma$ has limit type (see Definition 6.2 of their paper for a precise definition) then $\operatorname{Map}(\Sigma)$ cannot be generated by a coarsely bounded set.
A non-example: infinite rank
If $G$ is a finitely generated group, notice that all (a fortiori continuous) quotients of $G$ are finitely generated, and that conversely if $G$ has a quotient that is not finitely generated, then $G$ cannot be finitely generated. The same is true of Polish groups and coarsely bounded generation: if $G$ is a Polish group that has a continuous quotient which is not coarsely boundedly generated, then $G$ is not either. A prime example of such a group as a quotient is the countably infinite group $\bigoplus_{n = 1}^\infty \mathbb{Z}$ .
It is possible to build continuous maps to $\bigoplus_{n=1}^\infty \mathbb{Z}$ by using the topology of the end space. Here is one example. Consider the ends $\xi_n$ constructed in the previous post which are pairwise noncomparable. The $\xi_n$ are maximal ends of self-similar surfaces, so have stable neighborhoods. We form a surface by “fluting” together the union of countably infinitely many copies of each $\xi_n$ . Necessarily each collection of ends locally homeomorphic to $\xi_n$ converges to the maximal end of the flute. Now, this surface is self-similar, with genus zero or infinity, hence has coarsely bounded mapping class group. So take the connect sum of two copies of this surface, and call the connect sum $\Sigma$ .
As before, take a simple closed curve $\alpha$ that separates $\Sigma$ into two pieces, each one containing a single one of the two maximal ends. Pick one of the maximal ends, call it $\xi$ , and let $U$ be the neighborhood of $\xi$ determined by $\alpha$ . We claim that for each end $\xi_n$ and any mapping class $\phi$ belonging to the index-two subgroup of $\operatorname{Map}(\Sigma)$ fixing $\xi$ , the number of ends locally homeomorphic to $\xi_n$ mapped into and out of $U$ is finite. Indeed, were either quantity infinite, the same argument as in the previous example shows that $\phi$ would have to move $\xi$ .
Anyway, count up the number of ends of type $\xi_n$ moved into $U$ by $\phi$ and subtract the number of ends of type $\xi_n$ moved out of $U$ by $\phi$ . This defines a homomorphism $\ell_n \colon G \to \mathbb{Z}$ . By “shifting a strip of ends locally homeomorphic to $\xi_n$ ”, we can show that $\bigoplus_{n=1}^\infty \ell_n\colon G \to \bigoplus_{n=1}^\infty \mathbb{Z}$ is surjective, and continuous, since if $A$ is an annular subsurface with core curve $\alpha$ , the open set $U_A$ is contained in the kernel of $\bigoplus_{n=1}^\infty \ell_n$ .
This surface $\Sigma$ is an example of the general phenomenon Mann–Rafi term having end space of “infinite rank”. The argument we just gave generalizes to show that if $\Sigma$ has infinite rank (see Definition 6.5 for a precise definition) then $\operatorname{Map}(\Sigma)$ cannot be generated by a coarsely bounded set.