Rylee Alanza Lyman

Let’s once again fix a group $G$ that acts cocompactly on a tree $T$ . In the previous post we defined what it meant for an edge of $T$ to be surviving or collapsible. Collapsing orbits of collapsible edges in $T$ yields a new tree $T'$ which we say is obtained from $T$ by forest collapse. Two trees $T$ and $T'$ are in the same deformation space if there are $G$ -equivariant maps $T \to T'$ and $T' \to T$ . The set of $G$ -equivariant homeomorphism classes of trees in the same deformation space as $T$ all of whose edges are surviving is partially ordered under the operation of forest collapse, and this partial order contains minimal elements, which are reduced trees. To study this poset, or its geometric realization $L_T(G)$ , it would be convenient to understand all trees collapsing onto a given reduced tree. This is captured in the idea of an ideal edge, which I’d like to describe in this post. The idea of an ideal edge goes back to Culler and Vogtmann’s original paper on Outer Space; the treatment here is adapted from a paper of Krstić and Vogtmann.

Again we will work in the quotient graph of groups $\mathcal{G}$ , the construction of which we described in the previous post. We assume that $\mathcal{G}$ is finite and connected, and that if a vertex $v$ has valence less than 3, then at least one of the edge-to-vertex group inclusions $\iota_e\colon\mathcal{G}_e \to \mathcal{G}_v$ is not surjective. In tree language this says that $T$ is minimal and has no subdivision vertices. The graph of groups $\mathcal{G}$ is marked. If we fix a tree $T$ in the deformation space and identify $G$ with the fundamental group of its quotient graph of groups $\mathbb{G}$ , we may think of the marking as a homotopy equivalence in the sense of my paper $\sigma\colon \mathbb{G} \to \mathcal{G}$ .

Directions

Let $v$ be a vertex of $\mathcal{G}$ . Let $\operatorname{st}(v)$ be the set of oriented edges of $\mathcal{G}$ with initial vertex $v$ . The set of directions at $v$ , denoted $D_v$ , is the set

$ \coprod_{e \in \operatorname{st}(v)} \mathcal{G}_v/\iota_e(\mathcal{G}_e) \times \{e\}. $

The group $\mathcal{G}_v$ acts on $D_v$ on the left, and under the identification of $\mathcal{G}$ with the quotient graph of groups of $T$ , if $\tilde v$ is a lift of $v$ to $T$ , there is a $\mathcal{G}_v$ -equivariant bijection between $D_v$ and the set $\operatorname{st}(\tilde v)$ .

Suppose $T'$ is a tree such that collapsing the orbit of an edge $\tilde e$ incident to $v$ yields a tree equivariantly homeomorphic to $T$ . If we suppose that $T'$ is minimal, has no subdivision vertices and that every edge of $T'$ is surviving, we can make the following observations:

Furthermore conversely, if we have a subset of $\operatorname{st}(\tilde v)$ satisfying the above three properties, we can “blow up” the tree $T$ , inserting a new edge orbit $\tilde e$ .

Ideal edges

The idea of an ideal edge in $\mathcal{G}$ is designed to capture the above observations. To wit, an ideal edge based at a vertex $v$ is a subset $\alpha \subset D_v$ that is required to satisfy the following conditions. Let $\mathcal{G}_\alpha$ be the subgroup of $\mathcal{G}_v$ generated by the subgroups $g\iota_e(\mathcal{G}_e)g^{-1}$ for each direction $(g\iota_e(\mathcal{G}_e),e)$ contained in $\alpha$ .

We will say an oriented edge $e \in \alpha$ if there is some direction in $\alpha$ with underlying oriented edge $e$ . Notice that it follows from the conditions that $\alpha$ contains at least two oriented edges. Let $D(\alpha)$ be the set of oriented edges supporting a direction satisfying the third item above. If $\mathcal{G}$ is reduced and $\alpha$ is an ideal edge satisfying $\mathcal{G}_\alpha = \mathcal{G}_v$ , then $D_v - \alpha$ is also an ideal edge. The first item in the definition is clear. The second says that for each oriented edge $e \in \operatorname{st}(v)$ , either all directions with underlying oriented edge $e$ are in $\alpha$ or none are, which is also true of $D_v - \alpha$ . Since $\mathcal{G}$ is reduced, some and hence every edge $e \in D(\alpha)$ must form a loop based at $v$ (for otherwise we could collapse $e$ ), so we have $\bar e \in D(D_v - \alpha)$ . We call $D_v - \alpha$ the inverse of $\alpha$ . Two ideal edges $\alpha$ and $\alpha'$ are equivalent if there exists $g \in \mathcal{G}_v$ such that $g.\alpha = \alpha'$ .

An ideal edge $\alpha$ based at $v$ is contained in an ideal edge $\beta$ if there exists $g \in \mathcal{G}_v$ such that $g.\alpha \subset \beta$ . If $\alpha$ and $\beta$ are based at $v$ , the ideal edges are disjoint if $g.\alpha \cap \beta = \varnothing$ for all $g \in \mathcal{G}_v$ . If $\alpha$ and $\beta$ are based at different vertices, then they are disjoint. We say $\alpha$ and $\beta$ are compatible if one is properly contained in the other or if they are disjoint and not inverse.

Blowing up ideal edges

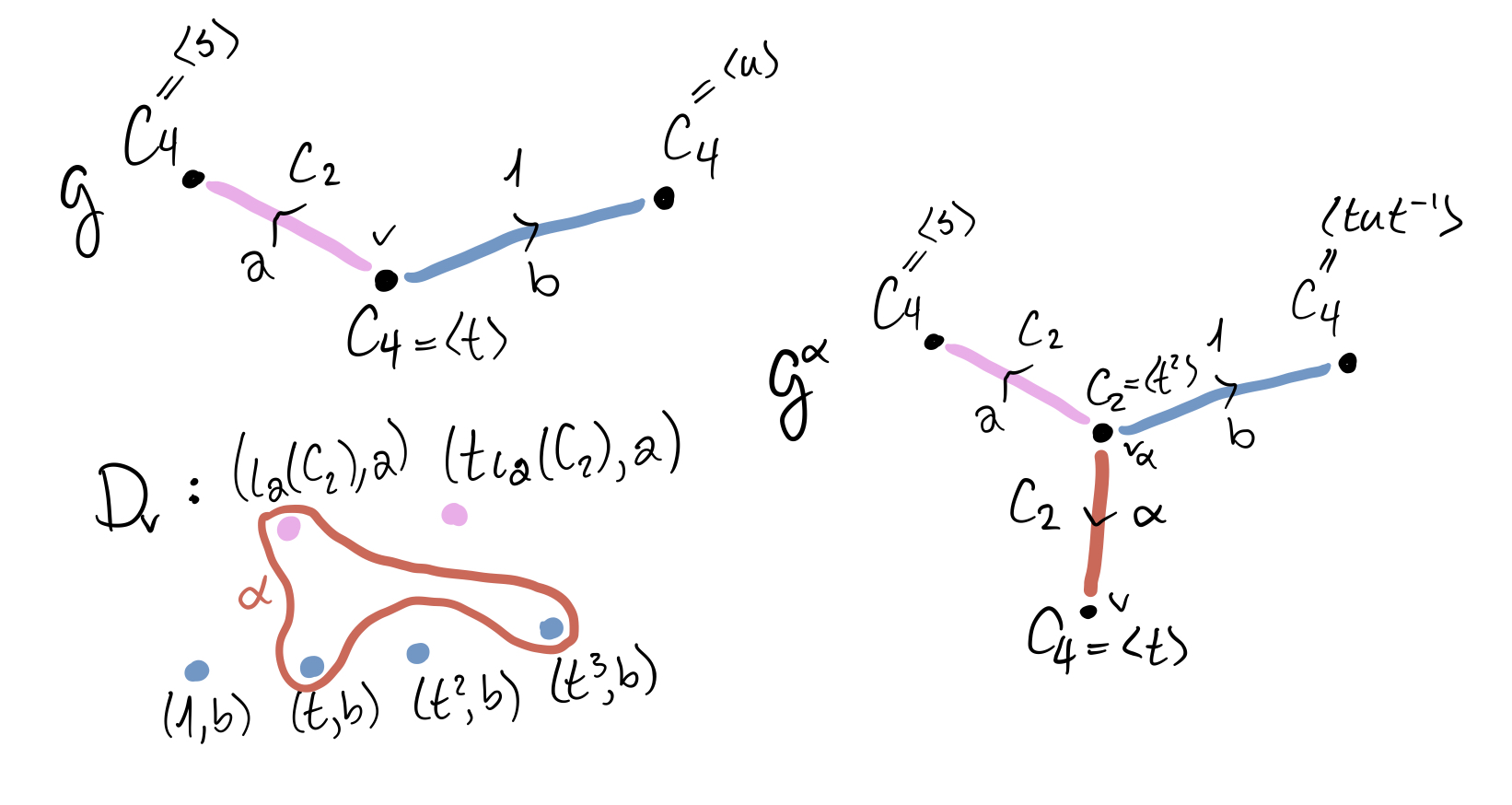
Blowing up an ideal edge in a graph of groups

Let $\alpha$ be an ideal edge of the marked graph of groups $\tau = (\mathcal{G},\sigma)$ . We construct a new marked graph of groups $\tau^\alpha = (\mathcal{G}^\alpha,\sigma^\alpha)$ by blowing up $\alpha$ as follows. The vertices and edges of $\mathcal{G}^\alpha$ are the same as the vertices and edges of $\mathcal{G}$ with one new vertex $v_\alpha$ and one new edge $\alpha$ ; the other vertices and edges are old. The old vertex and edge groups are equal to what they are in $\mathcal{G}$ . We have $\mathcal{G}^\alpha_{v_\alpha} = \mathcal{G}_\alpha = \mathcal{G}^\alpha_\alpha$ . The new edge $\alpha$ begins at $v_\alpha$ and ends at $v$ . If $e$ is an old oriented edge in $\alpha$ , then $e$ now has initial vertex $v_\alpha$ and the inclusion $\iota_e\colon \mathcal{G}^\alpha_e \to \mathcal{G}^\alpha_\alpha$ is obtained from $\iota_e\colon \mathcal{G}_e \to \mathcal{G}_v$ by recalling that we have $g\iota_e(\mathcal{G_e})g^{-1} \le \mathcal{G}_\alpha$ for some $g \in \mathcal{G}_v$ . Note that there is a choice here of group element $g$ ; differing choices will yield equivalent markings in a sense that I won’t make precise here. All other oriented edges have their initial vertices and edge-to-vertex group inclusions unchanged. There is a collapse map $\mathcal{G}^\alpha \to \mathcal{G}$ defined by collapsing the edge $\alpha$ and then “twisting” the edges incident to $v_\alpha$ by the corresponding choice of group element $g \in \mathcal{G}_v$ . We’ll describe maps of general graphs of groups in another post. Choose a homotopy inverse $f\colon \mathcal{G} \to \mathcal{G}^\alpha$ and define $\sigma^\alpha = f\sigma$ .

Observe that if $\beta$ is disjoint from (and not inverse to) or properly included in $\alpha$ , then $\beta$ may be regarded as an ideal edge of $\mathcal{G}^\alpha$ . If $\alpha$ are disjoint and not inverse, it’s not hard to see that $(\tau^\alpha)^\beta = (\tau^\beta)^\alpha$ .

An oriented ideal forest in a marked graph of groups $\tau$ is a collection of equivalence classes $\{\alpha_1,\ldots,\alpha_k\}$ of ideal edges in $\tau$ that are pairwise compatible. The ideal edges in an oriented ideal forest are partially ordered under inclusion. By repeatedly blowing up maximal elements of this partial order, we obtain a marked graph of groups $\tau^{\alpha_1,\ldots,\alpha_k}$ . Because each ideal edge $\alpha$ in a reduced marked graph of groups $\tau$ has an oriented edge in $D(\alpha)$ , it follows that each edge of $\tau^{\alpha_1,\ldots,\alpha_k}$ is surviving.

A pair of ideal edges $\alpha$ and $\beta$ are pre-compatible if they are compatible, or $\alpha$ is invertible with inverse $\bar\alpha$ and $\bar\alpha$ is included in $\beta$ . It follows that $\beta$ is invertible and that $\bar\beta$ is included in $\alpha$ . An ideal forest is a collection of pairwise pre-compatible ideal edges containing the inverse of each of its invertible elements. We can complete each oriented ideal forest $\Phi$ to an ideal forest $\Phi^\pm$ by adding the inverses of each of its invertible elements. Krstić and Vogtmann prove for graphs of finite groups as Lemma 5.7 of their paper that if $\Phi^\pm = \Psi^\pm$ as ideal forests in a reduced marked graph of groups $\tau$ , we have $\tau^\Phi = \tau^\Psi$ as marked graphs of groups. Again for graphs of finite groups, Krstić and Vogtmann prove as Proposition 5.9 that the poset of marked graphs of groups in $L_T(G)$ collapsing to a reduced marked graph of groups $\tau$ is isomorphic to the poset of ideal forests in $\tau$ .