Do you ever forget that a thing can happen? Like, imagine a quadrilateral, a shape with four edges. I bet the shape you imagined had the property of being convex, i.e. if you drew the two diagonals of the quadrilateral, those diagonals would actually be on the inside of the shape. Certainly this is true of my imagined quadrilateral. In fact, it takes me a minute to remember that I can imagine a shape that isn’t a rectangle or a parallelogram!

But there are quadrilaterals that are not convex; a “dart” shape might be a good example. Or like, take your favorite triangle, pick a side and imagine “pushing it in” a little to form two new sides. That’s a perfectly good quadrilateral that won’t be convex.

Now imagine you’re a computer trying to draw that quadrilateral all filled in. It’s funny how things that can go wrong in math often already go wrong very quickly. Like, there’s no bad way for a computer to draw a triangle, but shapes with four sides? Many ways to screw up.

As I said, it’s pretty easy for computers to draw filled-in triangles, and any quadrilateral can be cut—using its diagonals—into two triangles in two ways. But! for a non-convex quadrilateral, there’s a visually incorrect way of doing the cutting! In fact, there’s another way to screw up entirely!

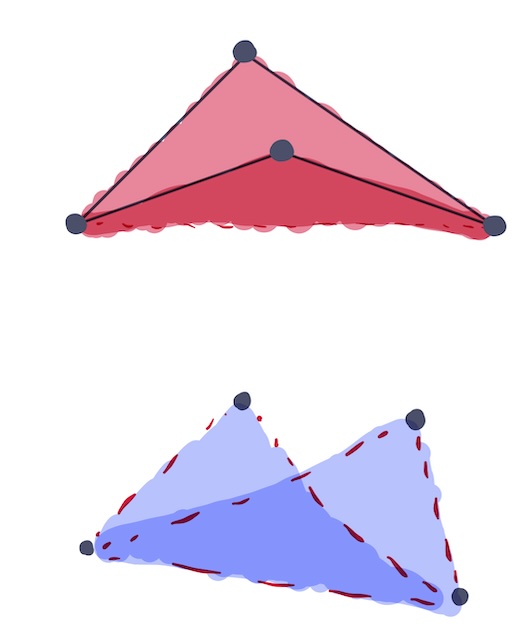
In the figure above, I’ve illustrated two ways things could go wrong. In the first one, the true “dart” shape is not drawn by the computer because we’ve chosen the wrong diagonal to cut the quadrilateral into triangles—the correct choice would be the diagonal which is contained inside the dart shape.

But in the second one, the computer chooses entirely the wrong triangles! Even though this quadrilateral is convex, we’ve managed to draw a kind of folded shape instead, because the computer doesn’t know that the repeated edge has to be a diagonal of the shape and not one of the edges.

For shapes that have more vertices, there are even more ways things can go wrong! Delaunay triangulation attempts to fix them.

Suppose we have a 2-dimensional shape with \(n\) points; Let’s clarify what we want: mathematically, the shape is a polygon of some sort—let’s assume at first that we don’t allow the construction of any holes. Then the shape, topologically, is just a disc, a filled-in circle. Of course, geometrically that’s very much not true, it’s got sides with straight edges and everything, but this is still a useful observation; here’s why: consider your favorite polygon. It’s got \(n\) vertices (three, say, for a triangle), \(n\) edges (right? if we order the vertices around the shape, there’s an edge from each vertex to the next one, which gives us \(n - 1\) of the edges, and then there’s one final edge from the last vertex back to the first one), and \(1\) face. There’s a cool topological property of two-dimensional shapes called the Euler characteristic, which we can compute by adding the vertices and faces and subtracting the edges: sometimes this is abbreviated symbolically as \(\chi = V - E + F\). Anyway, doing this for a polygon gives us \(n - n + 1 = 1\). The really neat thing here is that the Euler characteristic is a topological property; so anything that is topologically a disc will have \(V - E + F = 1\). So like, if you took a quadrilateral and subdivided it by drawing in the diagonal contained inside of it, now we have \(V = 4\), but \(E = 5\) and \(F = 2\), because we added one new edge and the one previous face now is two faces, and we see that \(V - E + F = 4 - 5 + 2 = 1\) is still true.

So. If we have \(n\) points which we are declaring to be vertices in our shape, we might hope to be able to compute the number of triangles our eventual triangulation will have. For quadrilaterals this is true: there will always be two triangles. But imagine adding a new vertex. If the new vertex is sort of “off to one side”, it makes sense to triangulate the resulting pentagonal shape with only three triangles—imagine triangulating a regular pentagon by drawing two “chords” from one vertex to the non-adjacent vertices.

But there’s another situation: if one of the vertices is “inside” the other four, then we need four triangles: like, imagine starting with a square and then declaring the point where the two diagonals cross to be a vertex.

So again, convexity is a core issue here. There are kind of two approaches to solving this. For a general mishmash of vertices, i.e. if we don’t assume that our vertices are sorted in some way, the choice to be non-convex seems pretty arbitrary. So in this case, let’s assume that the user wants the resulting shape to be more or less convex.

In the case of convexity, there is a neat triangulation called the Delaunay triangulation which we will produce. For a quadrilateral, the Delaunay triangulation could have as many as three triangles: what’s at issue here is the convex hull of the vertices, that is, the smallest convex shape that contains all of them. This shape could be a triangle (like it is for the dart) or a quadrilateral. We already know that we can triangulate a quadrilateral with two triangles, but if we put a vertex in the interior of a triangle, we have to split that triangle into three to produce a triangulation with four vertices.

The Euler characteristic is actually pretty useful here: Every edge of the triangulation that is an edge of the convex hull belongs to one triangle, while other edges belong to two. Therefore if the convex hull of \(n\) points has \(m \le n\) vertices, there are \(m\) edges that belong to exactly one triangle, and the actual triangulation we will produce can be obtained from the convex polygon by dividing faces.